Throughput analysis with Continuous-time Markov Chains simulations and…

Do you want our logo?

Do you want our logo description

At this moment a lot of companies offer end-point services (data providers, semantic analysis, ...) that we can integrate with our applications. However, when designing our own service, it could be tough find the ideal parameters to configure it and to find the best software to make it scalable and highly available.

Continuous-Time Markov Chains (Yin, G. et all, 1998) (CTMC) provides an ideal framework to estimate this most important parameters, and by means of simulations we can find them. An special model of CTMC which belongs to the Queuing Theory (Breuer, L. et all, 2005) is the M/M/c/K model, and modelize our service like a queuing system, implying that our system holds:

c: the number of parallel process
K: is the maximum number of clients waiting in the queue
Input: Poisson
Service: Exponential

E.g.: The next CTMC can represent a simple M/M/3/4 queuing system (Download .dot):

As seen in the picture above, grey nodes mean that n-3 clients exist waiting in the queue and the last state will be the red node (#7) which implies that at this moment incoming clients will be reject of our system.Like a CTMC we can derivate the equilibrium equations or we can use directly the formulae of the model M/M/c/K. By means of the software developed at ParadigmaLabs we are able to simulate several configurations on this model, and get other features too, e.g.:[java]M/M/c/K model simulation
------------------------ + MODEL PARAMETERS
Lambda: 40.0000
Mu: 30.0000
c: 3.0000
K: 7.0000
Stability: True (rho = 0.4444)

+ QUEUE
Average number of clients (l) = 1.4562
Average length (lq) = 0.1268
Average waiting time for a client into the queue (w) = 0.0365

+ SYSTEM
Average waiting time into the system (wq) = 0.0032

+ PROBABILITY DISTRIBUTION
P_0 = 0.2550368777
P_1 = 0.340049170234300
P_2 = 0.226699446822867
P_3 = 0.100755309699052
P_4 = 0.044780137644023
P_5 = 0.019902283397344
P_6 = 0.008845459287708
P_7 = 0.003931315238981
[Total Probability: 1.0]

Elapsed time: 0.00025105[/java]

Once we have calculated the best-fit values for our system, it is time to present our service based on a Wikipedia Semantic Graph. The next picture shows the main structure creating relations between articles and categories:

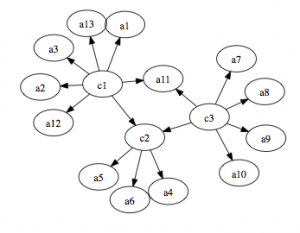
So, in first instance our service will perform lookup queries in order to identify Entities onto a text. We can see the result of a query to our service:

Up to this point, we have calculated several parameters for our system: Incoming Lambda (λ), Service Mu (μ), c (parallel servers) and K (queue length). To ensure the system holds these several constrains we should implement a two layers throttle system.

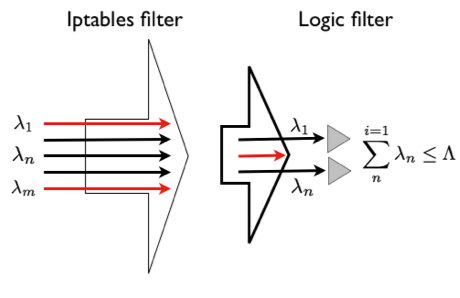
IPTABLES filter: Several clients will try to access to our system, however only a portion of them will succeed.
LOGIC filter: Is a software based filter and perform this throttle by means of user tokens. It applies temporal restrictions handling the incoming rate of each user.

Therefore, the following software help us to implement these restrictions:

Iptables filter: Using Iptables (debian-administration.org) we can restrict the incoming connections avoiding denial-of-service attack (DoS).
Logic filter: Using a time control and token manager script we can deal with this problem.
Several parallel servers and queue system: We set up Gunicorn to run several tornado servers to implement the queue restrictions.

[java]nohup gunicorn --workers 3 --backlog 7
--limit-request-line 4094 --limit-request-fields 4 -b 0.0.0.0:8000-k egg:gunicorn#tornado server:app &[/java] A sample tornado server scaffold for our service could be:
[java]>

-- coding: utf-8 --

import tornado.ioloop from tornado.web import Application, RequestHandler, asynchronous from tornado.ioloop import IOLoop \# Main class class NerService(tornado.web.RequestHandler): def get(self): \# run application app = tornado.web.Application(\[ (r"/", NerService, dict(...parameters...), \]) \# To test single server file" app.listen(8000) tornado.ioloop.IOLoop.instance().start()\[/java\]

Finally, after applying this configuration we have simulated several incoming rates (testing sundry numbers of clients too) getting the next service performance statistics represented in the picture below:

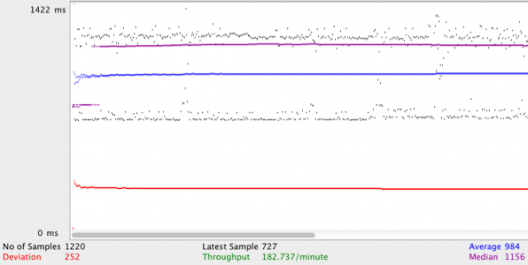
Summing up:

Using wikipedia categories and articles, we are able to detect a huge range of Entities.
Wikipedia is always updated in real time, therefore we have a updated NER (Name Entities Recognition).
We can use Gunicorn to run and manage serveral service instances.
We have implemented a throttle system to restrict the maximum number of requests per second. Also the way to restrict the general incoming rate by means of iptables is provided.
It is proven to be neccessary to simulate different invocations of our services using Queuing Theory formulae to find the best-fit paramaters like λ, μ, ρ, L, Lq, W, Wq.